6軸ロボットの逆運動学をsympyで解いてみよう

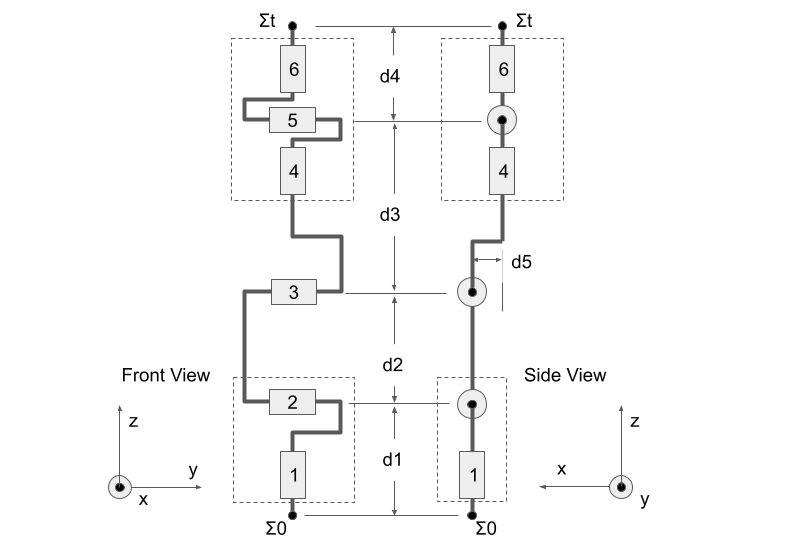
順運動学、逆運動学を解く前に、このような図を描いてロボットの自由度配置をきちんと定義しておくことが重要です。定義の仕方は一意ではないですが、ここでは以下のように定義しておきます。

回転関節は軸方向に長い円筒形で描かれていて、根本から関節1, 関節2, …,関節6,と6つの関節があります。すべての関節角度は図の姿勢で0度であるとします。

Σ0をベースリンク（根本）の座標系とします。ベース座標系は、ロボットの前方向がx軸、左方向がy軸、上方向をz軸と定義しています。Σtをツールリンク（手先）の座標系として定義し、原点位置はツールの先端とします。

ここに図示はしていませんが、各関節の回転後の子リンクにも座標系Σ1〜Σ6が定義されているとしましょう。各座標系はベース座標系と同じ向きを向いていて、各関節の回転中心に原点があるとします。ただし、点線で囲まれた関節は軸が直交していて、それらの座標系は同じ位置に原点位置が存在するものとします。
つまり関節1と2の座標系の原点は同じ位置(Σ0の真上にd1の高さの位置）にあるとします。関節4,5,6も直交しているので、それらの座標系の原点も同じ位置(関節5の回転中心上の位置）にあるとします。

以上のように定義すると、このロボットの座標変換は関節の角度theta1〜theta6と、関節間の距離のパラメータd1〜d5で定義できることが分かります。

ここで大事なことは、手首の関節4,5,6が直交していることです。この性質により比較的簡単に逆運動学を解くことができます。産業用ロボットアームの手首の3軸が直交していることが多いのはそのためです。